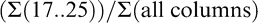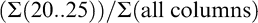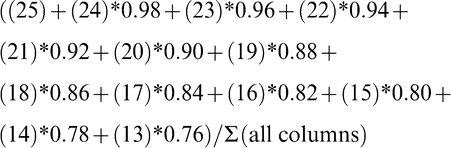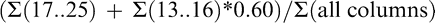Introduction

Incorrectly assessing peanut maturity at harvest can translate into tremendous economic losses not just to single growers but to the peanut industry as a whole. Peanut maturity affects not only yield through the accumulation of weight as the peanut matures, but determines crop quality (grade) and oftentimes flavor through the conversion of sugar into oil as the peanut seed develops (Fincher et al., 1980). In addition, an over-mature crop may lead to increased mechanical losses during the process of digging due to deteriorating peg strength with age. This mechanical loss, termed digging loss, is the retention of pods in the soil during the digging process due to separation of the pod from the stem attachment at the plant. Typical digging losses have been estimated to be 8% of the total yield but can reach 40% at dates beyond optimal maturity (Young et al., 1982; Lamb et al., 2004). Therefore, correctly assessing peanut maturity prior to digging is essential to the economic viability of peanut production.

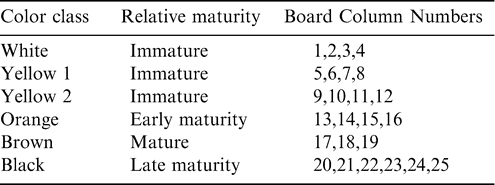
Over the past few decades, several methods have been used to assess peanut maturity with varying degrees of success and logistical application. These include: days after planting; Langley's Index; internal hull color (Shellout Method); oil color; methanolic extraction; kernel density; seed/hull ratio (SHMI); arginine maturity index (AMI); physiological maturity index; and the hull scrape method (Sanders et al., 1982a,1982b). While these methods of assessing peanut maturity have been used to varying degrees by peanut growers in the history of peanut production, the most widely and currently accepted method for the determination of peanut maturity is the “maturity profile board” based on the work of Williams and Drexler (1981). Williams and Drexler (1981) described the relationship of pod mesocarp color and texture (determined after the removal of the hull exocarp) with certain physiological stages of kernel development. They further detailed the temporal relationship of these various stages of development, making the projection of optimal harvest date possible. Williams and Drexler (1981) were the first to combine the observations of many researchers (e.g. Pattee et al., 1977 and 1980; Sanders et al., 1980) into a succinct peanut maturity profile board relating pod color classes with developmental stage. The currently utilized maturity board divides each large color class (white, yellow 1, yellow 2, orange, brown, and black) into individual columns that represent successive stages of development within these color classes (Table 1). It is recommended that five to six plants be randomly collected across a given field and 150–200 pods removed. The pod exocarp is then removed through either high pressure washing or sand blasting with glass beads under high pressure washing. Once the exocarp has been removed, pods are placed into individual columns based on the subjective classification of their mesocarp color. The percentage of pods within each color class and column is then used to determine the optimum digging date for that crop. This technique, to date, is the accepted and primary method utilized in most peanut production regions to determine crop maturity and predict the optimum digging date. While this method is accepted as the industry standard, it has three major drawbacks. First, while striving to provide a more objective estimation of maturity, the method still involves subjective assessment due to the required color separation of the blasted pods and is highly susceptible to an individual's ability to separate blasted pods into color categories. Second, the method is time consuming because it requires the collection of a destructive plant sample which must be further processed, and usually requires additional samples collected by the grower at weekly or less intervals until actual digging. Third, the method described by Williams and Drexler (1981) may or may not represent current peanut cultivars, especially late maturing cultivars, as it was developed for the mid-maturing cv. Florunner.

Alternative methods for assessing peanut maturity that can successfully predict an optimal digging date and can be practically applied by growers are very few. One possible alternative is the degree day or thermal heat unit method. This method, tailored to individual crop physiology, has been applied successfully to a wide array of crop species including: corn, soybean, cotton, vegetables, and peanut (Sanders et al., 1982b; NeSmith and Hoogenboom, 1994; Dufault, 1997; Perry et al., 1997; Andrade et al., 2000; Cober et al., 2001; Viator et al., 2005), and many natural species (Spano et al., 1999). While the method of predicting crop maturity using degree days has been used successfully in other crops and in peanut, no study has directly compared a degree day method to peanut maturity assessed using the accepted maturity profile board (Williams and Drexler, 1981). The ability to predict peanut maturity by applying the degree day or thermal heat unit method could provide an objective, accurate, and simple alternative to the more subjective and time consuming maturity profile board.

The objectives of this research were to: 1) create an index of maturity based on the distribution of peanut pods within the accepted maturity profile board classes that give the best quantifiable correlation with peanut yield and grade; and 2) test degree day models against such an index to determine their efficacy in predicting the optimum maturity index.

Materials and Methods

Planting and Crop Maintenance

Peanut (cv. Georgia Green) was planted in 2003 and 2004 at two research sites: one located in Dawson, GA and the other in Sasser, GA. The soil at Dawson was a Greenville fine sandy loam (Fine, Kaolinitic, thermic Rhondic Kandiudults); the soil at Sasser was a Tifton loamy sand (Fine-loamy, Kaolinitic, thermic, Plinthic, Kandiudults). These two soil types represent the predominant soils that peanuts are grown in Georgia U.S. At both sites, peanuts were sown in twin rows consisting of two planted rows (“twins”) 23 cm apart with a distance of 91 cm between the two twin rows. Inter-seed distance was 10 cm within each of the rows comprising the twin row. Seed were pre-treated with Vitavax®, an anti-fungal seed treatment (Gustafson, Plano, TX, USA). Disease control included foliar sprays of chlorothalonil and tebuconazole on a ten- to fourteen-day schedule starting 28–30 days after planting.

The Dawson site was not irrigated in 2003 but was irrigated in 2004 using an overhead lateral sprinkler irrigation system with scheduled irrigation based on a modified Jensen-Haise potential evapotranspiration (ET_o) calculation using atmospheric conditions. Estimated ET_o was multiplied by the crop coefficient for peanut (Harrison and Tyson, 1993) to estimate actual evapotranspiration (ET_a). If rainfall was greater than ET_a no irrigation was applied. ET_a amounts were added up over a 3–5 day schedule and subsequently applied using the lateral irrigation system. The Sasser site was irrigated in both 2003 and 2004 using subsurface drip irrigation (Toro Ag, Aqua-Traxx, Bloomington, MN, USA) installed 30 cm below the soil surface and with emitters spaced 30 cm apart. Individual emitter flow rate was maintained at 70 kPa at a rate of 1.0 liters per hour. Irrigation was scheduled with the same modified Jensen-Haise ET_o equation employed at the Dawson site but utilizing the atmospheric parameters measured at the Sasser site. ET_a amounts were replaced on a daily basis.

Atmospheric Monitoring

The following atmospheric conditions were monitored at both the Sasser and Dawson sites using a Campbell Scientific Instruments (Logan, UT, USA) datalogging system: precipitation, ambient air temperature, relative humidity, incident solar radiation, wind speed and direction, and soil temperature at 5, 10, and 20 cm depths. When sensors failed or data gaps occurred, data was used from a third weather station located at the USDA-ARS National Peanut Research Laboratory that was 5 km and 12 km from the Dawson and Sasser sites, respectively (Hoogenboom, 2000).

Harvest and Maturity Indices

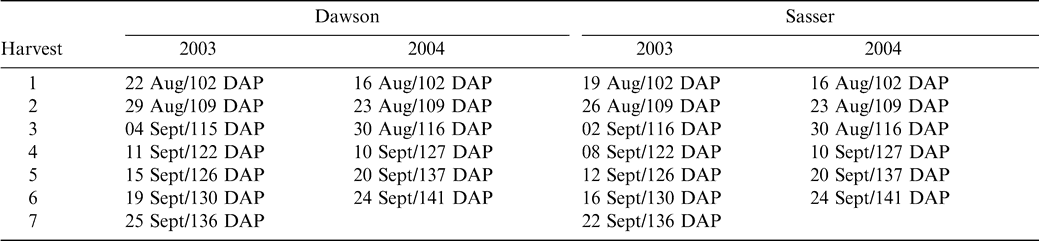
Test rows were harvested sequentially in 2003 and 2004 on a weekly basis or less as maturity progressed at each site (Table 2). At both sites, 2 paired twin rows were dug and inverted with a two row peanut inverter (Kelly Manufacturing Co., Inc., Tifton, GA, USA). These harvested rows were separated into three equal replicate sections (12 m each at Sasser and 9 m each at Dawson) and five plants were randomly collected from each replicate for maturity determination. The plants were returned to the laboratory and a sample of approximately 150–200 pods was removed. The exocarp was removed through the use of high pressure washing in the presence of glass beads in 2003, and through pressure washing using a rotating turbo nozzle in 2004. Blasted pods were placed on maturity boards and final color classes within individual columns (Table 1) determined by a single observer.

The color maturity board produces groupings of pods within individual color class columns, but it is not always clear what calculated percentage of color classes most closely represents crop maturity. Growers typically do not calculate any color percentages, but simply wait to harvest until at least three pods accumulate in the farthest black column. However, for the purpose of scientific examination, frequency distributions of pods based on color need to be calculated to produce an objective measure of crop maturity. To date, no study has examined the most effective index or combination of color classes on the board. In this study, harvest grade or percent total sound mature kernels (TSMK) was chosen as a surrogate for crop maturity because percent TSMK represents a combined measure of both yield (as reflected by weight) and the maturity of those kernels, and is known to increase linearly with crop maturity (Sholar et al., 1995). The higher the percent TSMK, the greater the distribution of kernel sizes in larger size classes, which are assumed to be of more advanced maturity (Emery and Gupton, 1968). In addition, TSMK is linked directly to the economic impact on the grower by determining the price per ton. To determine the best combination of color column percentages, the following maturity indices were calculated based on the sum of pods in individual columns of the maturity profile board (Table 1) as follows:

Maturity Index 1:

Maturity Index 2:

Maturity Index 3:

Maturity Index 4:

Maturity Index 5:

Maturity Index 6:

where numbers represent individual color columns and sums refer to the summation of all pods within a column (Table 1). Some indices represent a lumping of pods into larger color categories (yellow 1 to black; Maturity Index 1, 2, and 3) while others represent a minute division of pods into individual columns (Maturity Index 4, 5, and 6). It is assumed that the farthest black columns (columns 20..25) represent the most mature pods (Williams and Drexler, 1981). To take this into account in the more detailed calculated indices, less mature color categories were accounted for only by a percentage of their total frequency distribution.

The rest of each field replicate (containing inverted peanuts) was allowed to dry in the windrow for 2–3 days. Pods were then removed from the plants using a hand thresher (Kingaroy Engineering Works, Kingaroy, Australia). Pods were dried to between 7 and 10% moisture using either ambient or heated air flow in a 0.03 m³ dryer prior to the determination of field weight. A 1500 g sample of peanuts was randomly removed from each replicate sample, cleaned, and a 500 g sample removed for determination of a farmer stock grade. A farmer stock grade determines the kernel moisture, kernel size, and hull and kernel weight percentages, including TSMK. Final yield was determined by taking field weight and subtracting the weight of loose shelled kernels and foreign material, and correcting for moisture levels in excess of 7 percent. Digging losses, or those pods lost in the soil during the process of mechanical digging, were assessed during 2004. Soil within a 0.91 × 1.8 m² area was sifted through and pods remaining within a 15 cm depth collected. Digging loss pods within replicates were then individually scraped by hand to remove the exocarp and, based on mesocarp color, sorted into the larger maturity categories (yellow 1 to black) and then oven dried and weighed.

Calculation of Degree Days

Several accepted methods calculating degree days for peanuts were tested. Individual degree days were calculated on a daily basis utilizing meteorological data collected at both the Dawson and Sasser sites. Individual degree day methods were calculated as follows:

1. Emery method (Emery et al., 1969): DD1  =  (ATmax + ATmin)/2 − 13.3

2. Mills method (Mills, 1964): DD2  =  (ATmax₃₅ + 13.3 + ABS[ATmin − 13.3])/2 − 13.3 + ΔT_oc

3. North Carolina method 1: DD3  =  (ATmax₃₅ + ATmin_13.3)/2 − 13.3

4. North Carolina method 2: DD4  =  (ATmax₃₅ + ATmin)/2 − 13.3

5. West Texas method 1: DD5  =  (ATmax₃₅ + ATmin_12.8)/2 − 12.8

6. West Texas method 2: DD6  =  (ATmax₃₅ + ATmin)/2 − 12.8

7. West Texas method 3: DD7  =  (ATmax₃₅ + ATmin)/2 − 7.2

8. Bell-Wright method (Bell and Wright, 1998):

   If 9 ≤ ATavg ≤ 29, DD8  =  ATavg − 9

   If 29 < ATavg ≤ 39, DD8  =  20[1 − ((ATavg − 29)/10)]

   If ATavg < 9; ATavg > 39, DD8  =  0

9. Air temperature, soil temperature, and relative humidity method: DD9  =  ((ATmax + ATmin)/2 − 13.3) + ((STmax + Stmin)/2 − 18.3) + (90 − (RHmax + RHmin)/2)

10. Air and soil temperature method: DD10  =  ((ATmax + ATmin)/2 − 13.3) + ((STmax + STmin)/2 − 18.3)

where:

• ATmax  =  maximum daily air temperature

• ATmin  =  minimum daily air temperature

• ΔT_oc  =  ABS(ATmax − 24.4)

• ATmax₃₅  =  maximum daily air temperature, limited to high threshold of 35 C

• ATmin_13.3  =  minimum daily air temperature, limited to low threshold of 13.3 C

• ATmin_12.8  =  minimum daily air temperature, limited to low threshold of 12.8 C

• ATavg  =  (ATmax + ATmin) / 2

• STmax  =  maximum daily soil temperature at 5 cm depth

• STmin  =  minimum daily soil temperature at 5 cm depth

• RHmax  =  maximum daily relative humidity

• RHmin  =  minimum daily relative humidity.

The North Carolina and West Texas methods were determined from anecdotal information on degree day methods for those regions (C. Butts, pers. comm.). When testing for the correlation of degree days and peanut maturity, cumulative degree days (for each method) were calculated by summing daily degree days over the season up to each harvest date.

Data Analysis

Factorial analysis of variance (ANOVA) determined differences in yield and grade between years, harvest dates, and sites; and in pod digging losses (total and by color classes) between harvest dates and sites (SAS, 1997). Maturity indices were correlated with yield and grade (TSMK). Model fit was assessed using adjusted R², mean square error (MSE) and coefficient of variation (CV). For the maturity index that showed the strongest relationship with TSMK, a regression with net value (NV) was calculated to ensure the index was predictive of economic benefit to the grower. NV was calculated using the 2004 USDA Peanut Price Schedule for both locations and both years (USDA 2004). The official price schedule defines the yearly dollar value per percentage TSMK, loose shelled kernels (LSK), and other kernels and also defines deductions for excessive splits, damaged kernels, and/or foreign material. The value per kg may be multiplied by yield to give a net value per ha of the crop. The resulting net value represents the actual dollar value received by the grower and is thus a function of both quality and quantity (Blankenship et al., 2000).

Stepwise linear regression was used relating the leading maturity index with the various degree day models in combination with cumulative water applied and cumulative solar radiation in the model where significant. The best model was determined based on adjusted R², MSE, and CV.

Results

Maturity Index

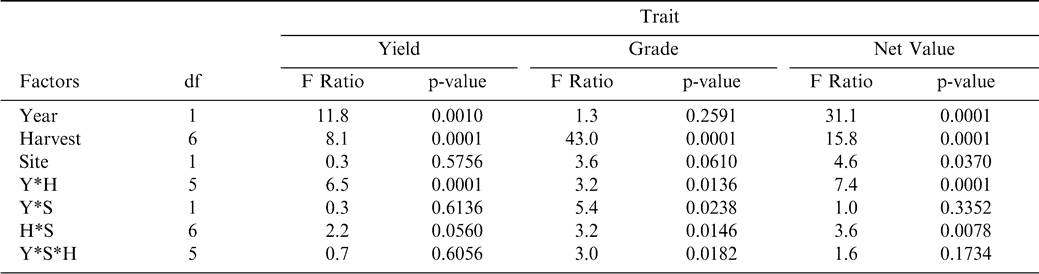
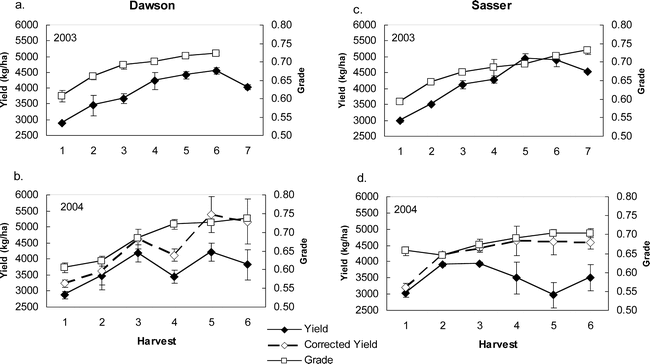
Peanut yield and grade were significantly different among harvest dates within each year, while these traits did not differ between the two sites of Dawson and Sasser (Table 3). Yield showed significant differences between years with yields higher in 2003 than in 2004 across the two sites (Figure 1). Grade consistently increased with each successive harvest at both sites in both years (although the 7^th harvest grade at Dawson was not analyzed) while yield tended to reach a maximum at the 5^th or 6^th harvest and then remain the same (as for the corrected yields at Sasser in 2004) or decrease to some degree (as at Dawson and Sasser in 2003; Figure 1).

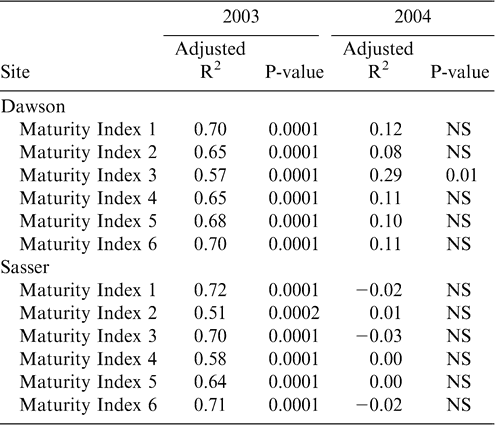
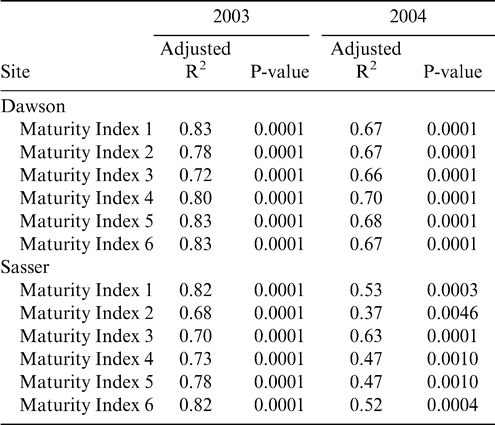
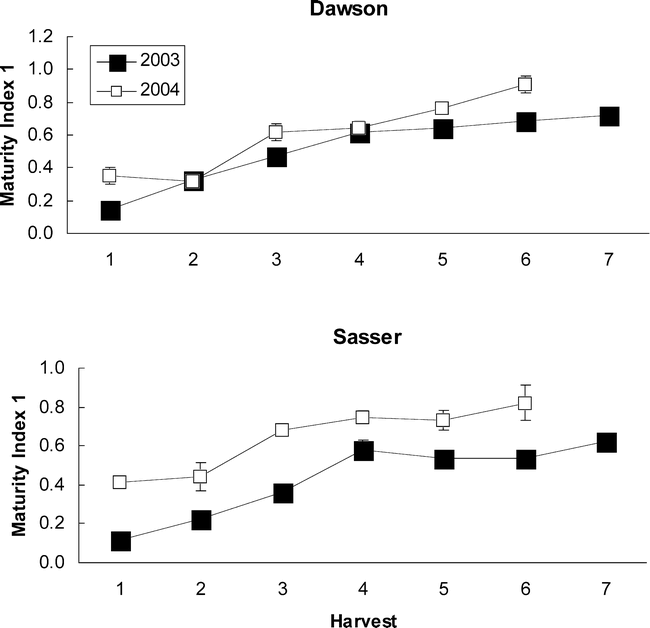
To determine the best index of maturity, individual maturity indices were correlated with both yield and grade. The Maturity Index 1, calculated as the percentage of black and brown pods, showed the best relationship with yield at both Dawson and Sasser in 2003 (Table 4); with only one index showing a significant correlation with yield (Maturity Index 3—the percentage of black pods) in 2004. However, grade represented the closest objective measurement of maturity, while yield was confounded with many other factors (including environmental effects) besides pod maturity. Therefore, the final assessment of maturity indices was made according to the adjusted R² values for the correlation between grade and the maturity indices (Table 5). As in the relationship with yield, Maturity Index 1 showed the best correlation with grade at both sites in 2003. In 2004, Maturity Index 1 showed overall consistently strong correlations with TSMK (adjusted R²  =  0.67 at Dawson and 0.53 at Sasser), but the adjusted R² value for Maturity Index 5 (0.68) at Dawson and Maturity Index 3 (0.63) at Sasser were greater. Because Maturity Index 1 showed the most consistently strong correlation with TSMK across sites and years, it was chosen as the best objective measure of peanut maturity. Maturity index 1 when calculated at both sites across harvests showed a steady overall increase in value in both 2003 and 2004 (df  =  6; F Ratio  =  63.2; p-value  =  0.0001) indicating the accumulation of mature black and brown pods as the crop approached its final maturity (Figure 2). Maturity index 1 was significantly higher in 2004 than in 2003 at both sites (df  =  1, F Ratio  =  88.9, p-value  =  0.0001).

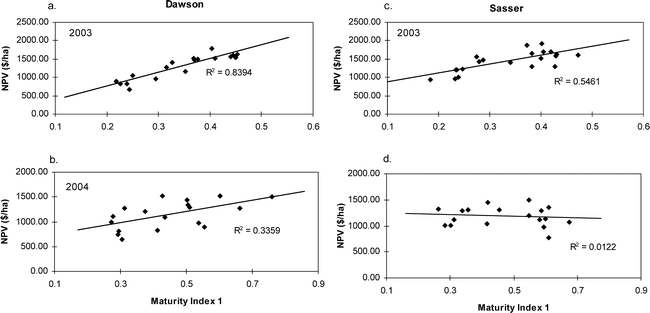
As with yield and grade, ANOVA for net value was significant for the year by location interaction (Table 3), therefore regressions were performed for each year and location. Net value showed a strong correlation with maturity index 1 in 2003, with R² values of 0.8394 and 0.5461 for Dawson and Sasser, respectively (Fig. 3). Dawson 2004 showed a greater correlation between net value and maturity index 1 when contrasted with Sasser, however, neither location was as strong as 2003.

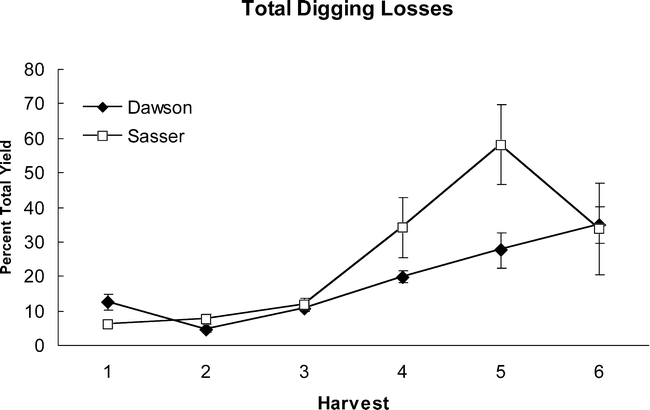
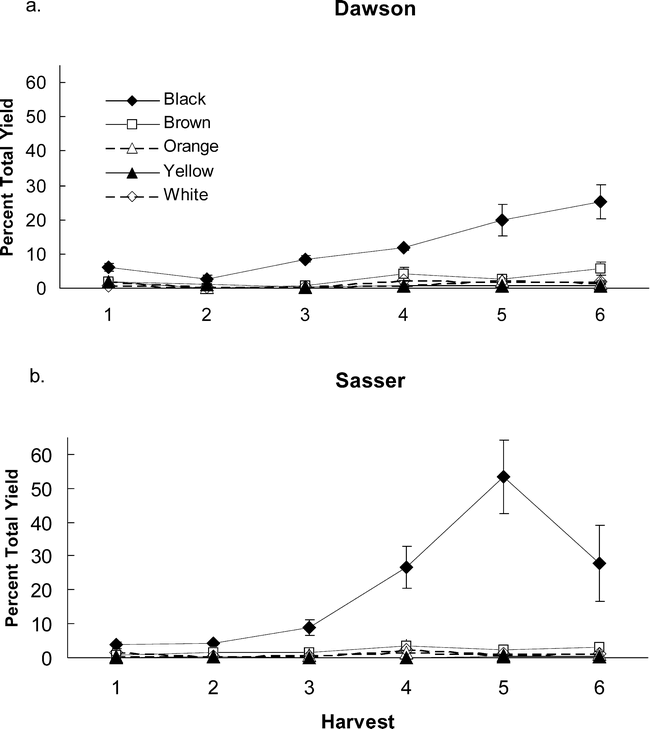
Part of the large decreases in yield noted at Sasser in 2004 (uncorrected yield line, Figure 1) can be accounted for by digging losses. Total digging losses did not differ between Dawson and Sasser (Table 6), but did increase in a linear fashion, with harvest date peaking in Dawson at the last harvest and in Sasser at the 5^th harvest (Figure 4). Total digging losses represented 35–50% of the total yield at both Sasser and Dawson. By adding these digging losses back into calculations of final yield for 2004, yield increases approach a steady level at Sasser, while showing increases for the 5^th and 6^th harvests at the Dawson site (Figure 1). Assessment of the maturity of the digging loss pods showed clearly that the majority of pod loss was from the most mature black class, with approximately 25% and 50% of total yield loss being black pods during some harvests for Dawson and Sasser, respectively (Figure 5). Overall, Sasser lost significantly more black pods than Dawson (Table 6). Black, brown, and white pod loss was significantly different among harvest dates. As with total pod loss, black pod loss increased nearly linearly at Dawson with the greatest losses occurring at the last (6^th) harvest; while the peak of black pod loss at Sasser was during the 5^th harvest (Figure 5).

Degree Days

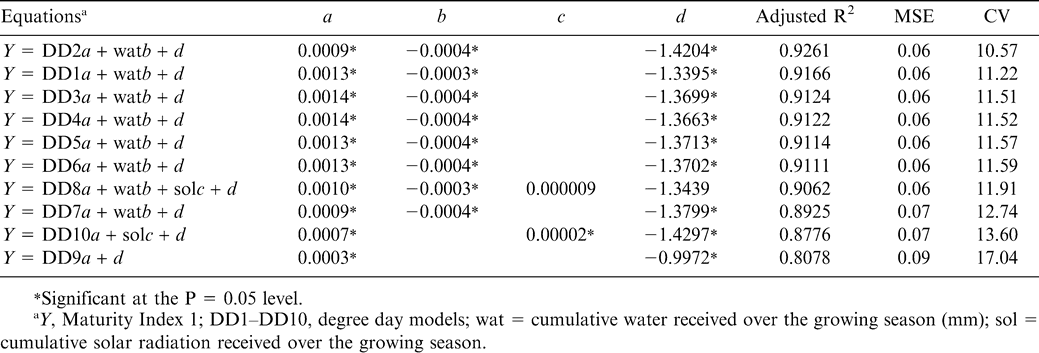
Out of all the degree day models tested in this study for peanut, the Mills method (DD2) incorporating maximum and minimum ambient temperatures with a lower threshold of 13.3 C and an upper threshold of 24.4 showed the best relationship with peanut maturity. With no environmental parameters added to the model, DD2 showed the best fit with Maturity Index 1 across years and sites (adjusted R²  =  0.9053). The addition of cumulative water application improved this model approximately 3% to a final adjusted R² value of 0.9261 (Table 7). Even though this model had the best relationship with Maturity Index 1, most of the previously established degree day models (DD1–DD8) showed adjusted R² values slightly above 0.90 with the addition of cumulative water amount or cumulative solar radiation. The models exhibiting adjusted R² values less than 0.90 included: DD7, the third model from west Texas incorporating maximum air temperature limited to 35 C, minimum air temperature and a lower threshold of 7.2 C; DD10 which incorporated maximum and minimum air and soil temperatures; and DD9 which incorporated maximum and minimum air and soil temperatures with relative humidity values (Table 7). All models had improved adjusted R² values with the addition of cumulative water, cumulative solar radiation, or both, with the exception of DD9.

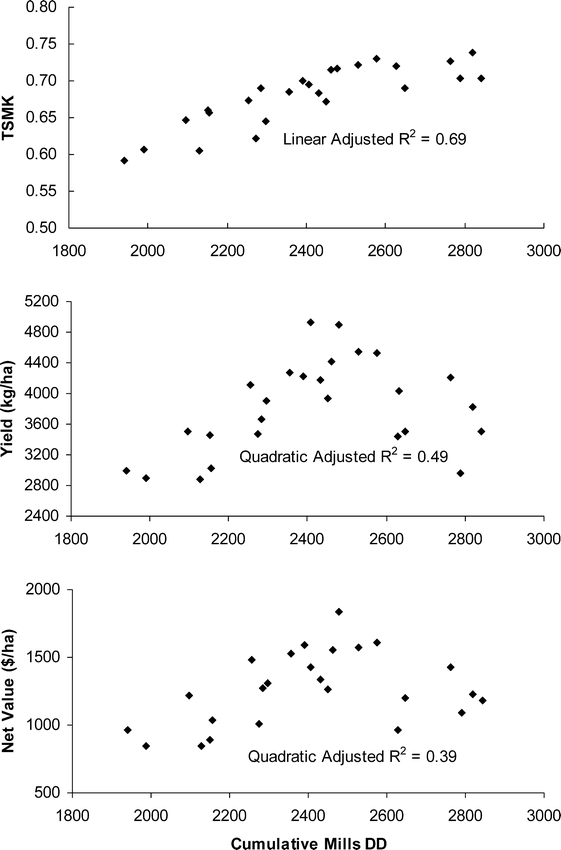
The relationship between the Mills degree day model (DD2) and TSMK, yield, and Maturity Index 1 was examined across years and sites to determine how robust the relationship was across differing environmental conditions. The DD2 model showed a linear relationship directly with grade (TSMK) with an adjusted R² value of 0.69 (Figure 6). The relationship of DD2 with yield was more complex. The linear relationship of DD2 with yield had an adjusted R² value of 0.09 while the non-linear, quadratic relationship was much improved with an adjusted R² value of 0.49; this shows yield as peaking with the accumulation of approximately 2400 Mills degree days and then tapering off with the accumulation of additional heat units (Figure 6). The relationship of DD2 with Net Value (NV) was also quadratic with an adjusted R² value of 0.39. The peak in NV was similar to yield, with accumulation of approximately 2400–2500 Mills degree days (Figure 6).

Discussion

Peanut maturity is a complex process involving shifts in assimilate partitioning throughout the plant. Overall, the biochemical processes occurring in the developing kernel involve a stabilization of protein content until the very last phase of peanut maturity, while throughout the maturation process, oil content increases and carbohydrate content decreases (Hung, 1994). Because of the complexity of the process and the fact that the developing peanut is shielded in the ground away from view, the prediction of peanut maturity has been a common problem faced by producers worldwide with dire economic consequences tied to an incorrect decision.

While this study does not challenge the validity of the accepted maturity assessment method, the maturity profile board (Williams and Drexler, 1981), the current results suggest some possible modifications that may improve the subjective nature of the method. The results from this study indicate that it may not be necessary to divide individual color classes (yellow 1, orange, brown, etc.) into individual color gradations represented by separate columns on the maturity profile board (Table 1) in order to make an accurate assessment of maturity. These classifications are very difficult and can vary widely depending on an individual observer's ability to distinguish fine color and texture gradations on the pod mesocarp. Maturity index 1, or the percentage of black and brown pods (summing all columns within these classes), was the best indicator of grade, and therefore economic return to the grower, compared with the indices that divided the color classes more finely. Yield was also correlated with Maturity Index 1 above the other more complicated indices (Maturity Index 4, 5, and 6). However, the relationship of the maturity indices with yield was much weaker than the relationship with TSMK, probably due to the strong dependence of yield on environmental conditions as well as length of time for crop development (Sanders et al., 1980). The superior assessment of Maturity Index 1 can be seen in the correlation with NV, as this represents economic impact on the farm level. A strong correlation in 2003 across both locations indicates that Maturity Index 1 could be used to select the most profitable harvest date.

Improving upon the logistical application of the peanut maturity profile board was certainly a goal of this study, but beyond this objective, identifying quantitative methods of assessing crop maturity that can be applied without the collection of plants was another important objective. One promising alternative was the degree day method, and this study has shown a clear correlative relationship with maturity assessment by the profile board and degree day accumulation. Degree day models utilizing soil temperatures have been used for predicting other production related processes in peanut including aflatoxin contamination (Thai et al., 1990) and crop coefficients (Kc) related to seasonal water use (Bandyopadhyay et al., 2005). The use of degree day models for peanut maturation is somewhat intuitive because for Arachis, as for many plants in general, the most important factor in the rate of overall plant phenological development is temperature (Bell and Wright, 1998). Pod development, specifically, is relatively sensitive to ambient air temperature in the range of 20–25 C and this temperature range generally enhances pod growth (Awal et al., 2003). This study showed that the best relationship with maturity was the degree day model DD2, which was the model first presented by Mills (1964) and based on a model developed by Gilmore and Rogers (1958) for corn. Although DD2 showed the best statistical fit (based on adjusted R², MSE, and CV values), the much simplified DD1 or Emery method (1969) also predicted peanut maturity with 90% accuracy. Ketring and Wheless (1989) found Emery (1969) accumulated degree days to range between 1450 and 1670 at final harvest; in general, the final harvest values for DD1 in the current study were somewhat higher, where values at Dawson were 1702 and1811 in 2003 and 2004, respectively, and at Sasser were 1625 and 1828 in 2003 and 2004, respectively. Further, Ketring and Wheless (1989) found the Emery (1969) method to be highly successful in predicting both vegetative and reproductive growth for Spanish and Virginia peanut genotypes. These results show that overall peanut plant development appears to be highly correlated with degree days, specifically to the Mills (1964) and Emery (1969) degree day methods.

The predictive capability of the DD1 and DD2 models with Maturity Index 1 was excellent with an adjusted R² value of 0.9043 and 0.9053, respectively. This relationship was improved for both models when cumulative water applied over the growing season was added into the model (adjusted R²  =  0.9166 and 0.9261 for DD1 and DD2, respectively; Table 7). Most other studies point to the importance of photoperiod as a partner with air temperature in determining crop maturity due to the reliance of carbon fixation (and therefore assimilate accumulation during maturation) on incident radiation. Accounting for cumulative solar radiation can be important because both temperature and light intensity play important roles in controlling development in crops (Ramesh and Gopalaswamy, 1991). Although temperature is the primary factor, photoperiod has been shown to modify the overall response of peanut pod maturation (Flohr et el., 1990). Total short-wave solar radiation during the growing season has been used for calculating values of thermal time to predict peanut development, and in fact, Bell and Wright (1998) found that nearly all of the variation in harvest index at one research site in Australia could be explained by the effect of photoperiod. However, in the current study, cumulative solar radiation turned out not to be significant in the stepwise regression models except in a few instances (DD8, and DD10); and was not the significant modifying factor in the best predictive model, DD2. In the relationship with DD1 and DD2, cumulative water received over the season (either through irrigation or precipitation) improved the relationship with Maturity Index 1 by almost 2% for both models. The importance of water to crop performance is not surprising, but its link to maturation has been less explored to date.

One interesting trend noted in this study was the quadratic relationship of cumulative DD2 with yield and net value (Figure 6). Yield and net value reached a peak after accumulation of approximately 2400 degree days and tapered off with additional degree day units. This may be reflective of a balance between maturity and yield, such that more mature pods may be lost as the peg attachment degrades with age and is manifested by decreasing yield. This same trend would be reflected in net value because this calculated variable takes both TSMK and yield into account simultaneously. The peanut crop (number of pods) is set over a period of 40–60 days (Ketring et al., 1982), so that at any given harvest time, there is a range of kernel ages on a single plant. Older pods necessarily have older peg attachments that could be weaker in strength, thus contributing to digging losses of pods at harvest. Yield may reach some maximum at a given degree day accumulation but then be counteracted by loss of extra-mature pods over time as maturity increases. Digging losses proved to be a significant impact in this study on the final yield determination and probably weakened the relationships of yield with the calculated maturity indices. Most of the pods lost were from the black class showing possibly the loss of peg strength with increasing time. This is the ultimate dilemma faced by the grower — striking a balance between quality grades and loss of over-mature pods.

The results from this paper present degree day models that can be applied successfully in the southeastern U.S. to runner-type peanuts. However, the application of these models in other peanut producing regions in the U.S. or across the world is limited and their utility should be validated under specific environmental conditions. For example, it was somewhat surprising that degree day model DD10, that took air and soil temperature into account, was not one of the more accurate methods because high soil temperature can significantly shorten times to podding and maturity (Awal et al., 2003). But perhaps this is a product of the southeastern U.S. environmental conditions where soil temperatures are generally high and not limiting to crop maturity. However, in environments such as west Texas U.S., where cool soil temperatures are experienced during some parts of the season, soil temperature incorporated into a degree day model may be very important. The limitation of applying degree day methods across regions has been previously found with other thermal calculation models and that their ability to accurately predict maturity across contrasting environments can be highly variable (Bell and Wright, 1998).

Literature Cited

Awal M. A. , Ikeda T. , and Itoh R. 2003 The effect of soil temperature on source-sink economy in peanut (Arachis hypogaea). Environmental and Experimental Botany 50 : 41 – 50 .

Andrade F. H. , Otegui M. E. , and Vega C. 2000 Intercepted radiation at flowering and kernel number in maize. Agron. J 92 : 92 – 97 .

Bandyopadhyay P. K. , Mallick S. , and Rana S. K. 2005 Water balance and crop coefficients of summer-grown peanut (Arachis hypogaea L.) in a humid tropical region of India. Irrig. Sci 23 : 161 – 169 .

Bell M. J. and Wright G. C. 1998 Groundnut growth and development in contrasting environments 2. Heat unit accumulation and photo-thermal effects on harvest index. Expl. Agric 34 : 113 – 124 .

Blankenship P. D. , Grice G. M. , Butts C. L. , Lamb M. C. , Sanders T. H. , Horn B. W. , and Dorner J. W. 2000 Effects of storage environment on farmer stock grade factors in an aerated warehouse in west Texas. Peanut Science 27 : 56 – 63 .

Cober E. R. , Stewart D. W. , and Voldeng H. D. 2001 Photoperiod and temperature responses in early-maturing, near–isogenic soybean lines. Crop Science 41 : 721 – 727.

Dufault R. J. 1997 Determining heat unit requirements for broccoli harvest in coastal South Carolina. J. Amer. Soc. Hort. Sci 122 : 169 – 174 .

Emery D. A. and Gupton C. L. 1968 Reproductive efficiency of Virginia type peanuts. II. The influence of variety and seasonal growth period upon fruit and kernel maturation. Oléagineux 23 : 99 – 104 .

Emery D. A. , Wynne J. C. , and Hexem R. O. 1969 A heat unit index for Virginia type peanuts. I. Germination to flowering. Oléagineux 24 : 405 – 409 .

Fincher P. G. , Young C. T. , Wynne J. C. , and Perry A. 1980 Adaptability of the arginine maturity index method to Virginia type peanuts in North Carolina. Peanut Science 7 : 83 – 87 .

Flohr M. , Williams J. H. , and Lenz F. 1990 The effect of photoperiod on the reproductive development of a photoperiod-sensitive groundnut (Arachis hypogaea L.) cv. NC Ac 17090. Expl. Agric 26 : 397 – 406 .

Harrison K. and Tyson A. 1993 Irrigation scheduling methods. Bulletin no. B-974 Ga. Agric. Exp. Stn Athens, GA .

Hoogenboom G. 2000 The Georgia automated environmental monitoring network. In Preprints 24^th Conference on Agricultural and Forest Meteorology, 24–25 American Meteorological Society Boston, Mass .

Hung Y. C. 1994 Effect of harvest date on the chemical composition of peanuts. Transactions of the ASAE 37 : 1287 – 1291 .

Ketring D. L. , Brown R. H. , Sullivan G. A. , and Johnson B. B. 1982 Growth physiology. 411 – 457 In Pattee H. E. and Young C. T. eds. Peanut Science and Technology Amer. Peanut Res. Educ. Society., Inc Yoakum, TX, USA .

Ketring D. L. and Wheless T. G. 1989 Thermal time requirements for phenological development of peanut. Agronomy Journal 81 : 910 – 917 .

Lamb M. C. , Masters M. H. , Rowland D. , Sorensen R. B. , Zhu H. , Blankenship P. D. , and Butts C. L. 2004 Impact of sprinkler irrigation amount and rotation on peanut yield. Peanut Science 31 : 108 – 113 .

Mills W. T. 1964 Heat unit system for predicting optimum peanut-harvesting time. Transactions of the ASAE 7 : 307 – 309,312 .

NeSmith D. S. and Hoogenboom G. 1994 Variation in the onset of flowering of summer squash as a function of days and heat units. J. Amer. Soc. Hort. Sci 119 : 249 – 252 .

Pattee H. E. , Wynne J. C. , Young J. H. , and Cox F. R. 1977 The seed-hull weight ratio as an index of peanut maturity. Peanut Sci 4 : 47 – 50 .

Pattee H. E. , Wynne J. C. , Sanders T. H. , and Schubert A. M. 1980 Relation of the seed/hull ratio to yield and dollar value in peanut production. Peanut Sci 7 : 74 – 77 .

Perry K. B. , Wu Y. , Sanders D. C. , Garrett J. T. , Decoteau D. R. , Nagata R. T. , Dufault R. J. , Batal K. D. , Granberry D. M. , and Mclaurin W. J. 1997 Heat units to predict tomato harvest in the southeast USA. Agricultural and Forest Meteorology 84 : 249 – 254 .

Ramesh P. and Gopalaswamy N. 1991 Heat unit requirement and prediction of developmental stages in soybean. J. Agronomy and Crop Science 167 : 236 – 240 .

Sanders T. H. , Lansden J. A. , Greene R. L. , Drexler J. S. , and Williams E. J. 1982a Oil characteristics of peanut fruit separated by a nondestructive maturity classification method. Peanut Science 9 : 20 – 23 .

Sanders T. H. , Schubert A. M. , and Pattee H. E. 1982b Maturity methodology and postharvest physiology. 624 – 654 In Pattee H. E. and Young C. T. eds. Peanut Science and Technology Amer. Peanut Res. Educ. Society., Inc Yoakum, TX, USA .

Sanders T. H. , Williams E. J. , Schubert A. M. , and Pattee H. E. 1980 Peanut maturity method evaluations. I. Southeast. Peanut Science 7 : 78 – 82 .

SAS 1997 SAS Institute Inc Cary, NC, USA .

Sholar J. R. , Mozingo R. W. , and Beasley J. P. 1995 Peanut cultural practices. 354 – 378 In Pattee H. and Stalker H. T. eds. Advances in Peanut Science Amer. Peanut Res. Educ. Society, Inc Stillwater, OK, USA .

Spano D. , Cesaraccio C. , Duce P. , and Zinder R. L. 1999 Phenological stages of natural species and their use as climate indicators. Int. J. Biometeorol 42 : 124 – 133 .

Thai C. N. , Blankenship P. D. , Cole R. J. , Sanders T. H. , and Dorner J. W. 1990 Relationship between aflatoxin production and soil temperature for peanuts under drought stress. Transactions of the ASAE 33 : 324 – 329 .

USDA, Farm Service Agency 2004 USDA Peanut Price Table. FSA-1007 U.S. Govt. Printing Office Washington, D.C., U.S.A .

Viator R. P. , Nuti R. C. , Edmisten K. L. , and Wells R. 2005 Predicting cotton boll maturation period using degree days and other climatic factors. Agronomy Journal 97 : 494 – 499 .

Williams E. J. and Drexler J. S. 1981 A non-destructive method for determining peanut pod maturity. Peanut Science 8 : 134 – 141 .

Young J. H. , Person N. K. , Donald J. O. , and Mayfield W. D. 1982 Harvesting, curing and energy utilization. 458 – 485 In Pattee H. E. and Young C. T. eds. Peanut Science and Technology Amer. Peanut Res. Educ. Society., Inc Yoakum, TX, USA .